前阵子两次面试,都被问到了逻辑回归的损失函数是什么,我知道是交叉熵,也很顺利的脱口说出了他的函数表达式,但是接下来被问到了为什么要用这个损失函数,我之前见过那张图,就是这个交叉熵函数的曲面是比平方损失函数(MSE)的曲面要陡峭,更方便梯度下降算法的迭代求解,但是再被往下深挖,问还有别的原因吗,这背后的存在的数学逻辑是什么?接着又被问了一堆的极大似然估计啥啥啥数理统计的东西,就有点说不出来了,所以查了一些资料,顺便写篇文章总结一下加深下理解。
交叉熵损失函数
先来熟悉下他的定义和函数形式,交叉熵(Cross Entropy)损失函数,也被称为对数损失函数,logloss,表现形式如下:
\[L=-[y\log(\hat y)+(1-y)log(1-\hat y)]\\\]
这里的\(y\)代表真实值,0或1,$y $代表预测值/估计值,值为一个概率,取值范围0~1,一般大于0.5我们就判定这个样本为1,小于0.5就把这个样本归为0。
从函数的形式上,我们可以看出,无论真实的\(y\)取0或1,这个加号两边的取值必有一个为0,假设\(y=1\),那么此时\(L=-\log(\hat y)\),此时损失函数代表预测为1的概率取负,如果\(y=0\),那么\(L=-log(1-\hat y)\),此时损失函数代表预测为0的概率取负,那么问题就简单了,直观上来理解这个损失函数,就是,要使得每一个样本属于其真实值的概率最大化。
虽然直观上理解这个损失函数代表的意义没有问题,但是其是怎么推导出来的呢?这样的形式会有什么样的优点呢?这里就有两种方式来理解这个损失函数了,一个是从数理统计的极大似然估计出发,另一个是从KL散度的角度出发。
从极大似然估计角度理解
极大似然估计
首先需要复习一下极大似然估计是什么玩意?这个东西虽然在本科的概率论和数理统计课程中就学过了,但是还是有那么一点一知半解。
要理解极大似然估计,就得先知道这个似然函数\(p(x|\theta)\)的概念,这个比较容易和概率函数搞混,因为表达式都是:\(p(x|\theta)\),但实际上似然函数(likelihood function )与概率函数(probability function)是完全不一样的两个东西。
如果\(p(x|\theta)\)中\(\theta\)是已知确定的,\(x\)是变量的话,那么这个函数就叫做概率函数,他描述在给定的模型参数\(\theta\)下,对于不同的样本点\(x\),其出现的概率是多少,比如对于身高的正态函数,给定参数均值170和标准差10,那么就可以计算出现身高为180的人的概率有多少。
反过来,如果\(p(x|\theta)\)中\(x\)是已知确定的,\(\theta\)是变量的话,那么这个函数就叫做似然函数,他描述对于不同的模型参数\(\theta\),出现$x $这个样本的概率是多少,还是身高的那个例子,如果给定一个样本身高为180,那么就可以计算不同的均值和标准差参数组合下出现这个样本的概率。
那么,极大似然估计是什么意思呢?就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值,举个例子,我给了一堆人的身高,这些样本都是独立同分布的,然后知道身高是符合正态分布的,我想要推出人群中身高的均值和标准差是多少,那么就可以通过遍历每一个参数值,然后根据似然函数算出每一个人身高对应的概率是多少,因为是这些人是独立同分布的,所以就可以通过把这些概率乘起来的方式,来计算出一个出现这些样本的概率,然后选取最大概率对应的那个均值和标准差,这个均值和标准差就是想要的结果了。
逻辑回归参数的极大似然估计
了解了极大似然估计,接下来就可以说一下啊逻辑回归的参数是怎么通过极大似然估计来进行估计的了。首先,根据逻辑回归的计算公式,我们可以知道对应为1和0的样本的概率:
\[\begin{align*}P(Y=1|x)&=\frac{e^{wx+b}}{1+e^{wx+b}}=p(x)\\ P(Y=0|x)&=\frac{1}{1+e^{wx+b}}=1-p(x)\end{align*}\]
然后就可以计算出现这些样本的似然函数,就是把每一个样本的概率乘起来:
\[L(w;b)=\prod_{i=1}^{n}[p(x_i)^{y_i}(1-p(x_i))^{1-y_i}\]
但是这个形式是连乘的,并不好求,所以一般我们会把他取对数,转化为累加的形式,就得到对数似然函数:
\[L'(w;b)=\sum_{i=1}^{n}[y_i\log(p(x_i))+(1-y_i)log(1-p(x_i))]\\\]
这时候呢,我们就可以通过最大化这个对数似然函数的方式来求得逻辑回归模型中的\(w\)和\(b\),把上面的式子加个负号,就是通过最小化这个负对数似然函数来求得\(w\)和\(b\),就可以通过梯度下降法来进行求解了。
可以发现,通过数理统计中的极大似然估计方法,也可以得到逻辑回归的损失函数。
从KL散度的角度理解
交叉熵是信息论里面的概念,要理解这里的交叉熵是怎么推出来的,就得先理解以下一个叫做KL散度(相对熵)的东西。
如果对于同一个随机变量\(X\)有两个单独的概率分布\(p(X)\)和\(q(X)\),那么我们就可以用KL散度来衡量这两个分布的差异:
\[D_{KL}(p||q)=\sum_{i=1}^{n}p(x_i)\log(\frac{p(x_i)}{q(x_i)})\\\]
我们将\(p(x)\)定义为真实的概率分布,\(q(x)\)定义为模型预测的概率分布,我们希望预测的概率分布与真实的概率分布差异越小越好,也就是使得KL散度越小越好,而\(p(x)\)是在数据集确定之后就确定下来的了,所以我们只要使得\(q(x)\)尽可能地接近\(p(x)\)就可以了。
将这个KL散度的公式展开可以得到:
\[\begin{align*} D_{KL}(p||q)&=\sum_{i=1}^{n}p(x_i)\log(\frac{p(x_i)}{q(x_i)})\\&=\sum_{i=1}^{n}p(x_i)\log(p(x_i))-\sum_{i=1}^{n}p(x_i)\log(q(x_i))\\&=-H(p(x))-\sum_{i=1}^{n}p(x_i)\log(q(x_i)) \end{align*}\]
学过信息论的可能会知道,\(-\log(p(x))\)代表的就是信息量,某一随机事件发生的概率越小,反映的信息量就越大,比如新冠疫情的发生,概率很小,但是蕴含的信息量就很大,而这个\(-\sum_{i=1}^{n}p(x)\log(p(x))\)代表的就是信息量的期望,也就是信息熵,然后如果把这个\(log\)里面的\(p(x)\)换成另一个分布的概率\(q(x)\),也就是\(-\sum_{i=1}^{n}p(x)\log(q(x))\),这个就是交叉熵。
所以根据上面那个展开的公式,就可以发现KL散度=交叉熵-真实分布的信息熵,而这个真实分布的信息熵是根据\(p(x)\)计算得到的,而这个\(p(x)\)是在数据集确定之后就确定下来的了,这一项就可以当成一个常数项,所以我们如果想让KL散度越小,只需要让交叉熵越小越好了,因此就可以直接将逻辑回归的损失函数直接定义为交叉熵。
使用交叉熵作为损失函数的好处
从上面的两个角度,我们就可以理解为什么逻辑回归要用交叉熵来作为损失函数了,但是,使用交叉熵背后的数学逻辑是明白了,那么,反映到实际里面,交叉熵到底有着什么样的优越性呢?
这里使用之前自己上数据挖掘课程ppt里的一张图来说明这个问题,可以看到,交叉熵函数的曲面是非常陡峭的,在模型效果差的时候学习速度比较快,是非常有利于梯度下降的迭代的,所以逻辑回归里面使用交叉熵作为损失函数而不是使用均方误差作为损失函数,这个也可以通过求导的方式来证明,不过限于个人水平,这里就不展开了,具体可以间文末列出的的第三篇参考资料。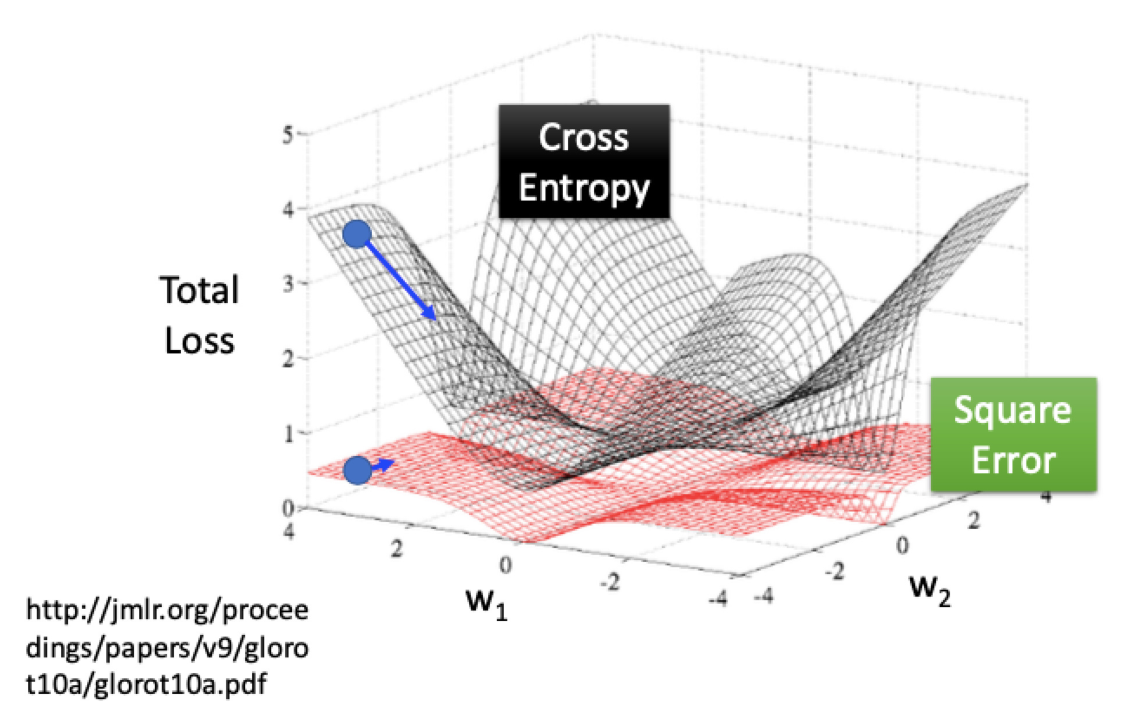
总结
本文主要从两个角度——数理统计的极大似然估计以及信息论中的KL散度,来说明逻辑回归中交叉熵函数背后的数学逻辑,同时也简单说明了交叉熵函数在逻辑回归中相对于均方误差函数的优势。